
No SolutionĪ system of equations has no solution when there exists no point where lines intersect each other or the graphs of equations are parallel. Similarly, for a system of linear equations in two variables, the unique solution is an ordered pair (x, y) which will satisfy both the equations in the system. Let understand the concept of a unique solution using a linear equation in one variable, 4x = 8 has a unique solution x = 2 for which the L.H.S is equal to the R.H.S.

The unique solution of a system of equations means that there exists only one value for the variable or the point of intersection of the lines representing those equations, on substituting which, L.H.S and R.H.S of all the given equations in the system become equal.įor example, we know that a linear equation in one variable will always have one solution.

There can be different types of solutions to a given system of equations, The main reason behind solving an equation system is to find the value of the variable that satisfies the condition of all the given equations true. We compute the values of the unknown variables still balancing the equations on both sides. We offer tutoring programs for students in K-12, AP classes, and college.Solving a system of equations means finding the values of the variables used in the set of equations. SchoolTutoring Academy is the premier educational services company for K-12 and college students. Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year. If -2x + 5/2 is ≥ 6, then x ≥ -1.75, and y is 2.5.įigure 3: Example of using elimination to solve a system of equations. The x variable is cancelled out to leave the inequality 3y + y ≥ 10, or 4y ≥ 10, or 2y≥ 5 so that y≥ 5/2.

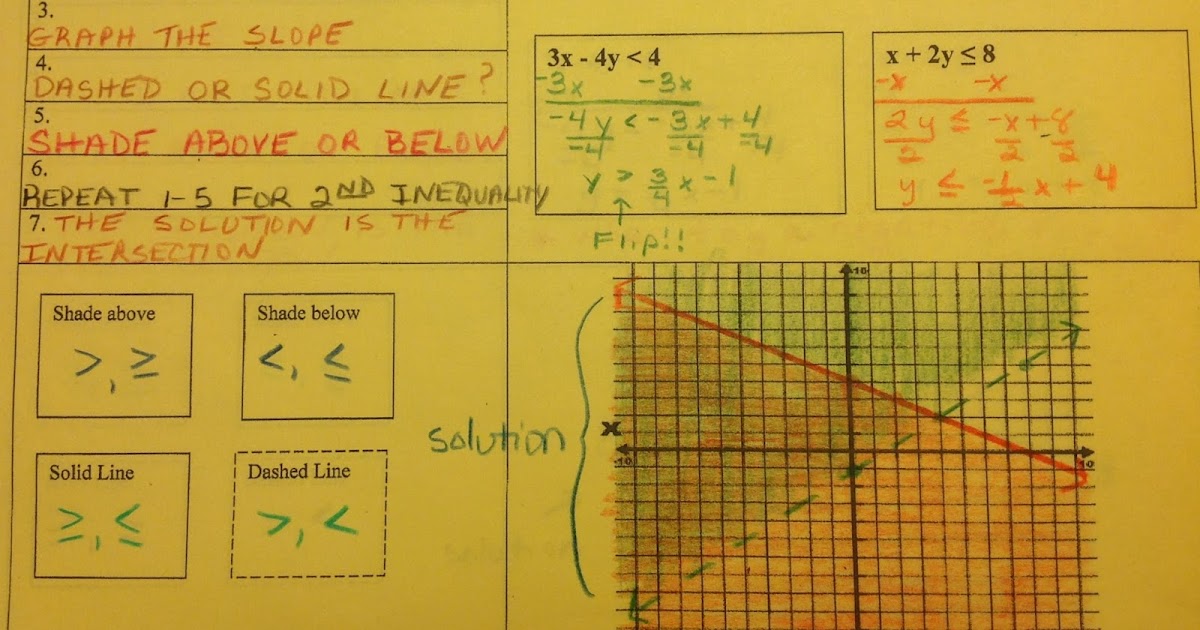
Suppose that the system of inequalities were 2x + 3y >4 and -2x + y ≥ 6. Solving Systems by EliminationĪlso, systems of inequalities can be solved using the elimination method. In that case y > 6 – 1 or y >5, when x = 3. Suppose that a pair of inequalities were represented by y > 2x – 1 and x = 3. Similar to equations, inequalities can be solved using the substitution method. The points that solve the system of inequalities are in purple, because they satisfy both the red and blue conditions.įigure 2: The solution set of a system of inequalities contains points that satisfy both conditions. Note that the blue inequality is shaded above the dotted line, as there is no equals sign, and the red inequality is shaded below a solid line, because there is an equals sign. If the inequality is x -3x + 5 is graphed and shaded in blue, and the inequality y≤ x – 2 is graphed and shaded in red. If the inequality is x≥ y, the solution set will include the points on the line x = y, as well as all the points above that line. If the inequality is x > y, the solution set for x = y will be represented by a dotted line, and then all the points that are above that line will be part of that solution set. The coordinates of the line for the solution set will pass through (0, 0), (1, 1), (2, 2) and so on. The solution set for an inequality appears as a section of the coordinate plane. The solution set for a linear equation appears on the coordinate plane as a line that contains all the ordered pairs that make the equation true. If the systems are solved graphically, or represented on the coordinate plane, the location of the solutions will depend upon the nature of the inequality. Similar to systems of linear equations, systems of linear inequalities can be solved graphically, by using substitution, or by using elimination.


 0 kommentar(er)
0 kommentar(er)
